Demonstration Video:

We will be partnering up with TechInDeep to bring you more Deep Learning Tutorials.

Before continuing with this post make sure to check out the ML.NET tutorial series:

Learn how to build neural networks from scratch:

• Neural Networks: Making Predictions Part 1
• Neural Networks: Making Predictions Part 2

Source Code Download:

• C# Neural Network

Programming Language:

• C#

What libraries we are going to use:

• We are not going to use any third party library.

Who is this article for:

• This article is for developers who would like to build their own neural network from scratch.

Additional Questions:

• You should post all questions here.

Workflow:

• First we will implement basic linear algebra operations
• Then implement feed forward logic
• Finally implement backpropagation algorithm
• Now we will be ready to implement basic XOR example

So let’s get started…

Table of Contents

Toggle

Matrix Math

Since we are going to implement the neural network algorithm from scratch, we would need basic linear algebra library. We can either download optimized one, or write it ourselves. In the download project I am including one very basic linear algebra library for you. All matrix operations are under the MatrixLibrary project.

In order to succeed at writing your first neural network, you will need to brush up on some basic linear algebra. Just make sure you are clear on matrix operations such as:

• Adding & subtracting matrices
• Multiplying matrices by scalars
• Multiplying matrices by matrices
• Transpose of a matrix

If you are familiar with these concepts then you are ready for the next section. Remember all matrix related code, and it’s implementation, can be found in MatrixLibrary project.

The Neural Network

In the sample project I am providing the neural network consists of: Input Layer -> Hidden Layer -> Output Layer as presented in the image

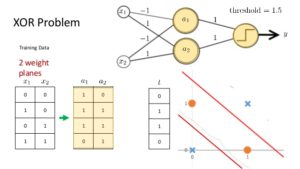
What we see here is that we have 2 inputs (X1 and X2), a hidden layer with 2 neurons (a1, a2) and an output layer that consists of only one neuron. On the image above, we can see the weights. They are located between the input layer and hidden layer, and the other weights are located between the hidden layer and the output layer. So if you do the math and do a FeedForward pass, you can see that the chosen weights between the layers are working exactly like they should. Once our neural network is trained, the weights between the layers should have the same effect.

Initializing the network

First we need to initialize our network weights to some random numbers. This is OK, because the backpropagation algorithm will update (change) the weights in order to “learn” the XOR operation. The weight initialization process requires it’s own article and explanation, but at this point, for this solution we just want to set up some random values. Let’s look at the code:

weights_0_1[i, j] = objRandom.NextDouble();   for the weights between the input layer and hidden layer and

weights_1_2[i, j] = objRandom.NextDouble();    for the weights between the hidden layer and output layer

Training the neural network

So now we have our weights initialized. But if we calculate the feedforward math, we will see that the result is not even close to what an XOR network should output. So let’s fix this.

In order to fix it, we need to train the network. We will train the network using the backpropagation algorithm. It all starts by deciding the value for our first two variables:

• Epochs which represents how many times we do: one forward pass and one backward pass of all training samples
• Learning Rate which is defined in the context of optimization, and minimizing the loss function of a neural network

We will cover all parameters in detail in some future post…

These variables are represented in the code as:

double learning_rate = 0.5;
int epochs = 2000;

Before updating the network weights, we first need to implement the so called ForwardPass.

FeedForward pass

These calculations are fairly simple. All we need to do is multiply two matrices and pass the result through activation function. So let’s see how to do this:

Matrix Layer_0 = Matrix.CreateRowMatrix(input);   – we create a row matrix from a double array.

Matrix Layer_1 = MatrixMath.Sigmoid(MatrixMath.Multiply(Layer_0, weights_0_1));

Here we can see that the first operation we execute is a matrix multiplication (Layer_0 with weights_0_1). The result of the operation (matrix) is passed down to an activation function. We do the same for the next layer.
Matrix Layer_2 = MatrixMath.Sigmoid(MatrixMath.Multiply(Layer_1, weights_1_2));

Matrix.CreateRowMatrix(double[] input) – function to convert a vector (double) array to a row matrix.

MatrixMath.Multiply(Matrix a, Matrix b) – function to multiply two matrices

Activation function

This topic will be discussed in detail in some future post. For now all we need to know about activation function is that is needed to do a complex non-linear mappings between the inputs and response variable. For this example I chose to use the Sigmoid activation function.

Backpropagation algorithm

In order to make the neural network learn the XOR operation we need to propagate the error back to the layer weights. In order to do that we simply calculate the error between the predicted value and the desired value.

Predicted value is the value that our neural network outputs

Desired value is the value we want the neural network to output

Let’s see how off our network is. Calculating the error is very easy. We use the following equation:

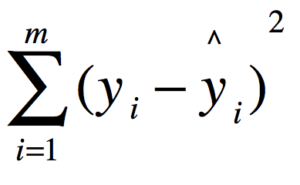
Or using C# code:

Matrix error = MatrixMath.Pow(MatrixMath.Subtract(Layer_2, desired_output_matrix), 2);

• Layer_2 is the predicted value that we get as a result of performing the Feedforward pass
• desired_output_matrix is the desired value, the value that we want our network to predict

Matrix Layer_2_delta = MatrixMath.ElementWiseMultiplication(MatrixMath.Subtract(Layer_2, desired_output_matrix),
MatrixMath.SigmoidDerivative(Layer_2));

Matrix Layer_1_delta = MatrixMath.ElementWiseMultiplication(
MatrixMath.Multiply(Layer_2_delta, MatrixMath.Transpose(weights_1_2)),
MatrixMath.SigmoidDerivative(Layer_1));

Calculating the Layer_1 and Layer_2 delta values. We basically calculate this for each layer except the output layer. This is where we use derivative of our activation function Sigmoid, to see how much we need to change the weights of the neural network. This explanation is too simple but we will have a detailed post on this subject as well…

Matrix weights_1_2_delta = MatrixMath.Multiply(MatrixMath.Transpose(Layer_1), Layer_2_delta);
Matrix weights_0_1_delta = MatrixMath.Multiply(MatrixMath.Transpose(Layer_0), Layer_1_delta);

Remember we need the change (delta) in the weights for each of our layer. So in this step we calculate the delta (change) for the weights.

Next we update our weights using the following code:

weights_0_1 = MatrixMath.ElementWiseSubtraction(weights_0_1, MatrixMath.Multiply(weights_0_1_delta, learning_rate));
weights_1_2 = MatrixMath.ElementWiseSubtraction(weights_1_2, MatrixMath.Multiply(weights_1_2_delta, learning_rate));

Instead of having a hard change in the weights, we control it using the learning rate we introduced earlier. So we multiply our learning rate with the weight delta matrix.

The mathematics and the detailed description will be provided very soon…

Complete Source Code: C# Neural Network

Learn how to build neural networks from scratch:

• Neural Networks: Making Predictions Part 1
• Neural Networks: Making Predictions Part 2