Hey guys, and welcome to “Neural Network making Predictions” series.
Today we will continue where we left off. Making predictions with multiple outputs. However, before you continue make sure you have a firm grasp on Part 1.
Neural Network making Predictions: multiple outputs with single input
In order to continue where we left off. Let us look at another simple example. A neural network with only one input, but multiple outputs.
So let’s take one input – “Win/Loss Record” as input variable. The output variables will be: “Fans Morale”, “Board Morale” and “Win Prediction”
- “Fans Morale” is how happy the fans are with the current “Win/Loss Record”. It can range between 0 and 10.
- “Board Morale” is how happy the team management is with the current “Win/Loss Record”. It can range between 0 and 10.
- “Win Prediction” given the current “Win/Loss Record” what is the probability for a win. It ranges between 0 and 1.
Side Note
Even though we are talking about percentage, the number we are calculating in “Win Prediction” is not a real percentage. We will see how we can convert this number into a real percent once we introduce Activation Functions.
The most important note to take home from this current network setup, is that we are making three different and independent predictions. The three output variables are correlated with the “Win/Loss Record” input, but make the prediction/decision independently.
What this means is that the fan happiness for a give “Win/Loss Record” can differ from the board management happiness. In addition, the third output has nothing to do with happiness. But given the current “Win/Loss Record” it needs to calculate what is the probability for a win.
Let’s look at some code.
double winLossRecord = 0.85;
double[] weights = { 0.8, 1, 0.9 };
double[] output = elementwiseMultiplication(winLossRecord, weights);
Console.WriteLine($"Win/Loss Record: {winLossRecord}");
Console.WriteLine($"Fans Happiness: {output[0]}");
Console.WriteLine($"Board Happiness: {output[1]}");
Console.WriteLine($"Win Prediction: {output[2]}");Code for the “elementwiseMultiplication” is provided bellow:
private static double[] elementwiseMultiplication(double scalar, double[] vector)
{
double[] output = new double[vector.Length];
for(int i = 0; i < vector.Length; i++)
{
output[i] = scalar * vector[i];
}
return output;
}And the output is:

So what is the output telling us?
- “Fans Happiness” we are calculating using 0.8 as the respective weight in the weights vector. In conclusion, fans are happy but they will never be 100% satisfied (this is because of the weight assigned)
- “Board Happiness” we are calculating using 1 as the respective weight in the weights vector. In other words, board is happy as long as the team wins. It has a direct correlation with the “Win/Loss Record”
- “Win Prediction” we are calculating using 0.9 as the respective weight in the weights vector. Therefore, this prediction is highly correlated with the winning streak of the team.
You can set the weights however you like (for now) to get the desired results. I do encourage you to play with the Input and Output parameters.
However, the important thing to extract from this example is that we calculated each output independently.
Introducing the “element wise multiplication”
We are at a point where we need to introduce a little bit of math.
If you have trouble with this concept please refer to the following link.
Or you can check this Khan Academy Article, and Basic Linear Algebra for Deep Learning
From the code listed above, element wise multiplication is an operation that multiplies each element of the vector with the scalar provided.
Neural Network making Predictions: multiple outputs with multiple inputs
Finally we are ready to create a very small Neural Network. Neural Networks consists of multiple inputs and multiple outputs. So this is a big milestone.
In order to improve our predictions, we need to use multiple inputs. So let’s merge what we learned in Part 1 and Part 2 of this tutorial.
Our input variables will be: “Number of players on team”, “Average years of experience” and “Win/Loss record”. Based on this input vector, we will predict three outputs as well: “Fans Happiness”, “Board Happiness”, “Win Prediction”
Let’s look at the visual representation of the network
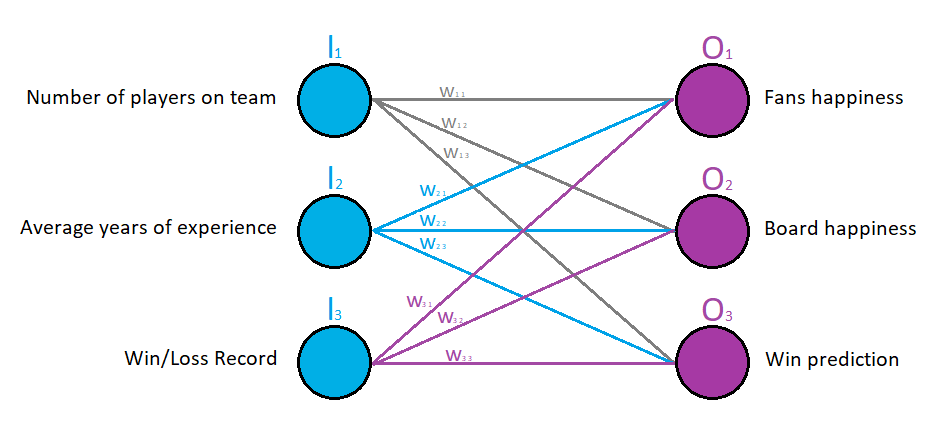
The very obvious thing we can state just by looking at the image, is that each input node (I) is connected to each output node (O) with a weight line (W).
Weighted Sum
private static double weighted_sum(double[] vector1,double[] vector2){
if (vector1.Length != vector2.Length) throw new Exception("Vector sizes must match!");
double result = 0;
for(int i = 0; i < vector1.Length; i++)
{
result += vector1[i] * vector2[i];
}
return result;
}The concept of “Weighted Sum” is very simple. We need it because we want to calculate the value for one output node, in a situation where we have multiple inputs and multiple outputs.
So where do we use the “Weighted Sum”?
Let’s look at the following example. Let input vector be I1=[0.1, 0.2, 0.3] and a weight vector W1=[0.4, 0.5, 0.6]. To calculate the weighted sum all you have to do is multiply the elements at their respective position and sum over them.
But what did we calculate in terms of our neural network?
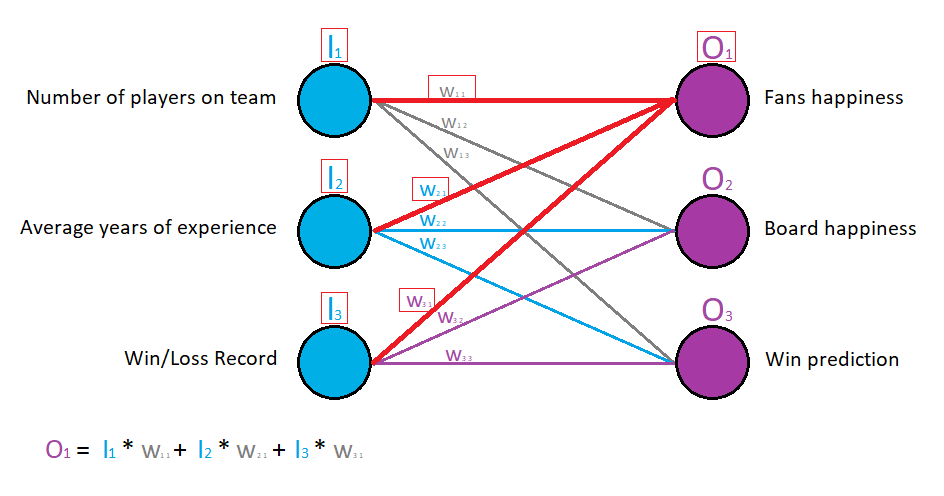
From the image above it’s obvious that we are calculating the value for the output node O1. O1 depends on the input vector [I1, I2, I3]. Like we stated in the previous tutorial (Part 1), each input value is multiplied with a corresponding weight. The weight is the value that is amplifying or reducing the input signal. And this is important, because different input value, impacts an output differently. For example the input “Number of players on the field” may have very small impact on the “Board Happiness” output. If you can’t grasp the intuition here make sure you check Part 1 of this tutorial.
So O1 is calculated by multiplying all input nodes with their respective weights and then summing over them. All elements involved in the calculation is marked with red color in the image above.
Now let’s get back at out example. Given the Input vector [0.1, 0.2, 0.3] and Weight vector [0.4, 0.5, 0.6] the weighted sum is calculated as:
0.1 * 0.4 + 0.2 * 0.5 + 0.3 * 0.6 = 0.32
Vector Matrix Multiplication
OK, so even though this looks like a different concept from what we have looked so far, it is not. Again a very simple procedure that will make our code cleaner in the long run.
private static double[] vector_Matrix_Multiplication(double[] vector, double[,] matrix){
if (vector.Length != matrix.GetLength(1)) throw new Exception("Vector and matrix size do not match!");
double[] output = new double[vector.Length];
for(int i = 0; i < vector.Length; i++)
{
double[] matrix_row = Enumerable.Range(0, matrix.GetLength(1))
.Select(x => matrix[i, x])
.ToArray();
output[i] = weighted_sum(vector, matrix_row);
}
return output;
}This concept is very helpful in Neural Networks because it is a lot cleaner (there are other benefits that we will explore later on).
*Linear Algebra Side Note
As you can see by now, Linear Algebra plays a big role in the way we calculate things. If some of these concepts are unclear, make sure you refresh your knowledge on some high school linear algebra concepts. That’s all for now.
Let’s see how we can represent this concept visually.
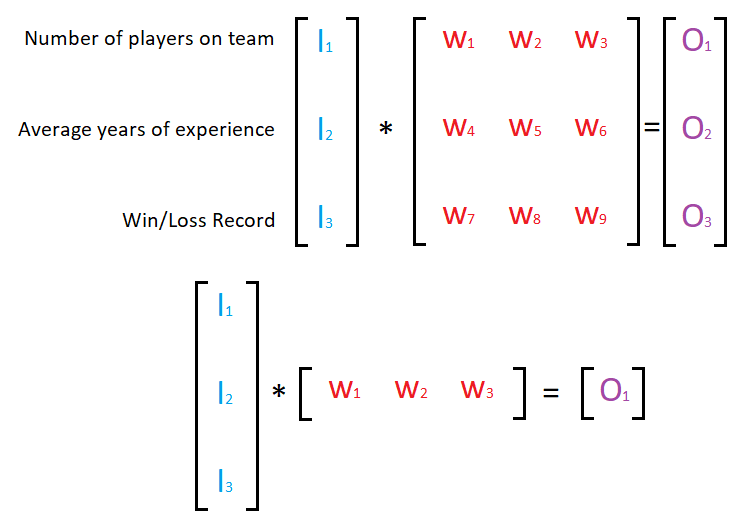
From the image above we can see that we are calculating the weighted sum for the input vector and each row from the weight matrix. The result for each weighted sum multiplication. actually represents the respective output node.
* Side Note
This is not the correct way to represent and calculate vector matrix multiplication operation. I am doing it this way just so that we keep the code and explanation clean. Right now its all about the intuition. We will see later how to do a proper matrix multiplication operation.
Neural Network making Predictions: The Forward Propagation
All of this leads us to the following code block
double[] input_vector = { 5.5, 0.6, 1.2 };
double[,] weights =
{
{0.5,0.1,-0.2 },
{0.9,0.4,0.0 },
{-0.2,1.3,0.1 }
};
double[] prediction = vector_Matrix_Multiplication(input_vector, weights);So the prediction becomes a single line code block.
As you can see it becomes harder for me to set the weights to get the desired result for our “Team Example”. Try it yourself. Try to set the weights values so that you get the desired outcome in our example.
This is what neural networks do. Every single training iteration they constantly improve the weight values so that the input is correlated with a desired output. You can imagine the weights as knobs (like on a radio). You move it until you get the right signal for some radio station. Well in a nut shell, that’s what a neural network does. It moves those knobs to get the desired output. More on that later…
We are not done yet. In order to create a “deep neural network” what we do usually is we stack layers upon layers. Join me next week where we are going to stack couple of layers to get a “deeper” network.
Related Posts:
You can download the complete project here.
vpn special code
March 31, 2024 at 9:38 pmMy coder is trying to convince me to move to .net from PHP.
I have always disliked the idea because of the costs.
But he’s tryiong none the less. I’ve been using Movable-type on numerous websites for about a year and am concerned about switching to another platform.
I have heard excellent things about blogengine.net.
Is there a way I can transfer all my wordpress
posts into it? Any help would be really appreciated!
my webpage vpn special code
vpn coupon 2024
April 1, 2024 at 7:43 amWhat i do not realize is actually how you’re no longer really much more neatly-preferred than you might be now.
You’re very intelligent. You recognize therefore significantly in relation to this subject, produced
me for my part believe it from so many varied angles.
Its like men and women are not involved unless it’s something to do
with Woman gaga! Your own stuffs excellent. All
the time take care of it up!
Here is my site … vpn coupon 2024
vpn coupon 2024
April 8, 2024 at 1:14 amIts like you learn my thoughts! You seem to grasp so much approximately
this, like you wrote the book in it or something. I believe that you
just can do with a few % to power the message home a bit, but other than that, that is magnificent blog.
A great read. I’ll definitely be back.
Feel free to visit my homepage :: vpn coupon 2024
vpn special coupon
April 10, 2024 at 7:12 amWhy users still make use of to read news papers when in this technological globe everything is accessible on net?
Feel free to visit my web page … vpn special coupon